Cerebral circulation model for multiscale blood flow analysis

Cardiovascular diseases such as cardiovascular diseases and cerebrovascular diseases that occur in the vascular system are mainly caused by vascular lesions such as arteriosclerosis and cerebral aneurysms. As a cause of these vascular lesions, mechanical stimulation of the blood vessel wall by blood flow is considered [1]. Therefore, grasping the influence of the flow field caused by the shape of the blood vessel is important in predicting the onset.

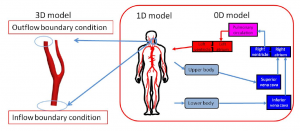
In three-dimensional blood flow analysis, it is necessary to calculate considering the influence of whole-body vascular network, capillary vessels, etc. Therefore, multi-scale analysis to couple the vascular network formed from mm to μm in size using different calculation methods Tokuda [2] conducted a study to give the pressure calculated from the 1-dimensional, 0-dimensional peripheral blood vessel model as the boundary condition of the 3-dimensional cerebrovascular vessel. However, in reality, the blood inflow conditions of three-dimensional analysis also change due to the blood flow resistance of peripheral blood vessels and so on, so the problem remains in fixing the inflow condition of three-dimensional analysis. Therefore, it is desired to calculate the boundary condition of the three-dimensional model from the systemic circulation of blood. Liang [3] Hara analyzed the whole-body circulation in which whole-body blood vessels were modeled as one-dimensional or zero-dimensional (Liang model) in order to calculate the boundary condition of the three-dimensional model from the systemic circulation of blood ). By this, it became possible to analyze the case where there was a vascular lesion such as stenosis somewhere in the body.

Fig.1: 3D-1D-0D Multi-scale cardiovascular system

Figures 2 and 3 show the distribution of flow rates at each vessel of the arterial circle of Willis with or without occlusion, respectively. The values are at the peak of systole.

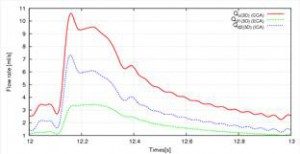
In this study, two types of calculations are performed: (i) Liang model and (ii) cerebral circulation model, and the effect of blood circulation calculation on three dimensional analysis was compared. Figures (2) and (3) show flow waveforms in the carotid artery. From these results, it can be seen that by considering the cerebral circulation, there is no inversion of the flow rate of ICA and ECA. This is because in the Liang model, one dimensional model is applied to one vessel on the ICA side, whereas in the cerebral circulation model it is considered that one dimensional model is applied to the Willis artery rings . That is, in the Liang model, the Willis artery rings are not reproduced, the peripheral resistance of the 0 dimensional model is strong and affects the flow waveform. On the other hand, since the cerebral circulation model reproduces the geometry of the Willis artery rings, the influence of compliance is also added from the zero dimension, and since the peripheral resistance on the ICA side is smaller than the Liang model, the blood It seems that it became easy to flow.

Fig.2: Flow Rate Waveform (i) (Liang model)

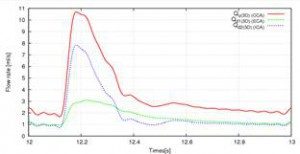Fig 3: Flow Rate Waveform (ii) (Cerebral circulation model)

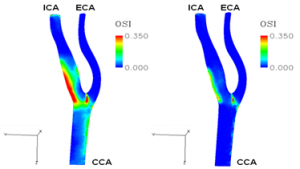
Figures (4) and (5) show the distribution of Oscillatory Shear Index (OSI) proposed by Ku et al. [4]. OSI is an index indicating the rate at which the direction of wall shear exerted by the blood flow on the blood vessel wall changes spatially with the pulsation of blood flow. From Figs. (4) and (5), it was confirmed that inclusion of the cerebral circulation model narrows the high region of OSI on the ICA side. This is thought to be due to the fact that the cerebral circulation model is present, the temporal change of the flow waveform becomes gentle and the change of the direction of flow decreases.

Fig 4: OSI Distribution (i) (Liang model) Fig.5: OSI Distribution (ii) (cerebral circulation model)

References

[1] Shojima, M. et al., Stroke, Vol.35, 2004, pp.2500-2505.

[2] 徳田茂史ら, 日本機械学会論文集（B編), 74 巻740 号(2008-4).

[3] F.Y.Liang, et al., J Biomech 42,692-704(2009)

[4] V. Milisic, et al., Math Model and Numer Anal 38,613-632(2004).