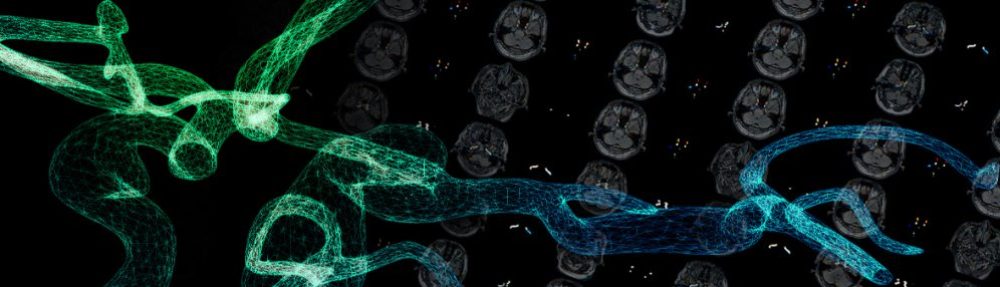
Fluid-structure interaction (FSI) analysis of aneurysm model considering deformation of blood vessel wall

Dynamic factors such as wall shear stress due to blood flow are said to be involved in the onset and rupture of cerebral aneurysms. In order to accurately predict wall shear stress in the living body by simulation, it is necessary to accurately reproduce hemodynamics in the living body. In general, the blood vessel wall is treated not as a rigid body but as a deformable tissue having elasticity, and the flow path is deformed from the viewpoint of blood flow. In order to carry out a blood flow simulation faithfully simulating the in vivo environment, it is necessary to consider such deformation of the blood vessel wall. Therefore, in this study, we perform a fluid structure coupled analysis to reproduce the interaction between fluid force due to blood flow and deformation of blood vessel wall.

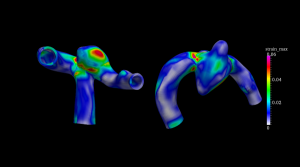
Figure 1 shown below is a visualization of the result of the flow velocity vector of fluid-structure interaction analysis in a middle cerebral aneurysm obtained from a medical image of a patient. From this figure, it is understood that there are many blood having a slow flow rate in the luminal cavity.

 

 

 

 

Fig.1: Flow velocity vector in middle cerebral aneurysm

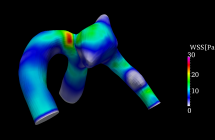
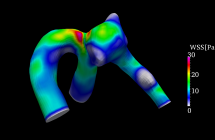
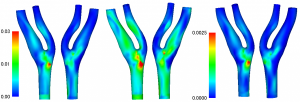
Figures 2 and 3 show the distribution of the wall shear stress at the peak of the beat obtained from the simulation result of the middle cerebral aneurysm. Fig. 2 shows the results of Fluid Structure Interaction (FSI), and Fig. 3 shows the analysis result of only fluid. As shown in the figure, the fluid-structure coupled analysis considering only fluid analysis and deformation of the blood vessel wall shows that the distribution of wall shear stress distribution is different. In particular, the gradient of the shear stress distribution of the wall surface was remarkably different in the neck portion of the nodule was obtained.

 

 

 

 

Fig. 2 Fluid-structure interaction analysis Fig. 3 Fluid analysis

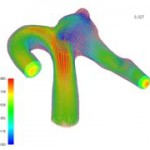
Figure 4 plots the distribution of the largest principal strain of the vessel wall at peak. As described above, not only fluid but also index of structure such as strain and stress can be evaluated in fluid-structure interaction analysis. In this figure, it is found that the strain strongly appears at the neck portion of the root of the nodule.

Fig.4 Maximum principal strain distribution at pulsation peak

In fluid-structure interaction analysis, the material properties of the structural part are also important. In general, it is said that the material property of a blood vessel wall is a nonlinear superelastic body, and the relationship between stress and strain is not linear. In the analysis of the middle cerebral aneurysm in the above figure, a non-compressed superelastic model called Mooney-Rivlin body was adopted. In FIG. 5 shown below, the structural analysis is performed by changing the model of the superelastic body in the carotid artery. It can be seen that the magnitude and distribution of displacement obtained by the material model used greatly changes.

Fig.5 Displacement distribution in the carotid artery (difference depending on material model)

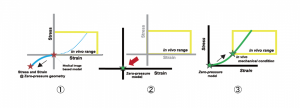
The deformation behavior of the blood vessel wall in the fluid structure coupled analysis can be greatly changed depending on the stress state in the blood vessel shape at the time of acquiring the medical image but it is difficult to set the initial condition because it is impossible to measure the stress state. Fig. 6 shows a method for setting the initial conditions of the stress state by estimating the blood vessel shape in the blood pressure unloaded state by the negative pressure load. We assume the material properties of the blood vessel wall as a nonlinear elastic material whose stress-strain relation is symmetrical at the origin and uniformly add negative pressure corresponding to the blood pressure at the time of acquiring the medical image to the inner wall of the blood vessel (①). After that, resetting the stress and strain generated in the vessel wall (②), loading the pressure equivalent to the blood pressure evenly over the blood vessel wall (③), reproduces the stress state in the blood vessel shape at the time of acquiring the medical image.

Fig.6 Estimation method of blood vessel shape under no load condition with negative pressure load

 

 

References

1. 片桐賢吾,　石上雄太,　大島まり,　山本創太,　流体-構造連成手法を用いた患者個体別頸動脈の解析,　第26回数値流体シンポジウム（東京2012）

2. Ryo Torii, et al., Int. J. Numer. Methods Fluids, Vol. 65, ( 1-3):pp.324-340, 2011.