心疾患・脳血管疾患をはじめとする血管系に生じる循環器系疾患は動脈硬化症や脳動脈瘤などの血管病変が主要因となっている.これらの血管病変を引き起こす原因の一つとして,血流による血管壁への力学的刺激が考えられている[1] .そのため,血管形状に起因した流れ場の影響を把握することが発症の予測の上で重要である.
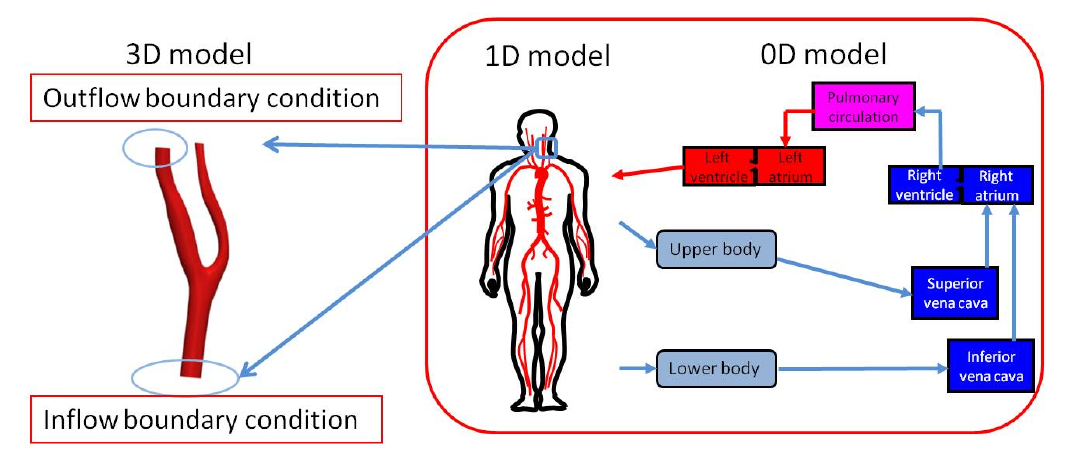
3次元血流解析では,全身の血管網や毛細血管等の影響も考慮した計算が必要となるため,mmからμmのサイズで形成される血管網を異なる計算手法を用いてCouplingするマルチスケール解析が必要となる. 徳田[2]は,1次元,0次元の末梢血管モデルから算出された圧力を3次元の脳血管の境界条件として与える研究を行った.しかし,現実には,末梢血管の血流抵抗等によって3次元解析の血液流入条件も変化することから,3次元解析の流入条件を固定していることに課題が残る.そこで,血液の全身循環から3次元モデルの境界条件を算出することが望まれている.Liang[3]はらは,血液の全身循環から3次元モデルの境界条件を算出するため,全身の血管を1次元や0次元にモデル(Liangモデル)化した全身循環の解析を行った(図1).これにより,体のどこか一部に狭窄などの血管病変があった場合の解析が可能となった.
Fig.1: 3D-1D-0D Multi-scale cardiovascular system
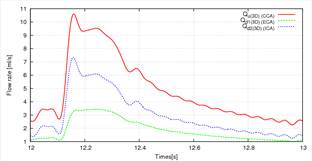
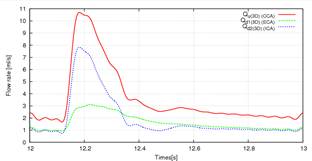
本研究では,(i) Liangモデル,(ii) 脳循環モデルの2種類の計算を行い,血液循環計算が3次元解析に及ぼす影響について比較した.図(2),(3)は頸動脈内の流量波形を示す.この結果から,脳循環を考慮することにより,ICAとECAの流量の逆転が起きていないことがわかる.これは, LiangモデルではICA 側で1本の血管に対して1次元モデルを適用しているのに対して,脳循環モデルではWillis動脈輪に対して1次元モデルを適用しているためと考えられる.つまり,LiangモデルではWillis動脈輪が再現されておらず,0次元モデルの末梢抵抗が強く流量波形に影響している.一方,脳循環モデルはWillis動脈輪の幾何形状を再現しているため,コンプライアンスの影響も0次元より加味され,またLiangモデルと比較してICA 側の末梢抵抗が小さくなったため,ICA側へ血液が流れやすくなったと考えられる.
Fig2: Flow Rate Waveform (i) (Liang モデル) Fig3: Flow Rate Waveform (ii) (脳循環モデル)
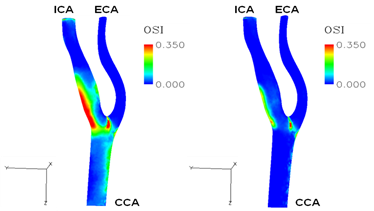
図(4),(5)にKuら[4]によって提唱されたOscillatory Shear Index (OSI) の分布を示す.OSIとは,血流の拍動に伴い血流が血管壁に及ぼす壁面せん断の方向が空間的に変化する割合を示す指標である.図(4),(5)から,脳循環モデルを含めるとICA側のOSIの高い領域が狭くなることを確認した.これは脳循環モデルがあることにより,流量波形の時間変化が緩やかになり流れの向きの変化が減少したことが影響していると考えられる.
Fig.4: OSI Distribution (i) (Liangモデル) Fig.5: OSI Distribution (ii) (脳循環モデル)
本研究では,1次元,0次元モデルを用いて脳循環を含む全身循環モデルを開発し,循環解析で得られた圧力,流量の情報を3次元解析の境界条件として与えるマルチスケール血流解析コードを開発し,動脈硬化症の好発部位である総頸動脈分岐部に対して解析を行った.脳循環を含めた全身の血液循環を考慮したマルチスケール血流解析を行った結果,脳循環のない場合と比較すると,ICAとECAの流量の逆転が改善されていることがわかる.また,流量波形の変化が緩やかになり ,OSIの高い領域が狭くなることを確認した.
参考文献
[1] Shojima, M. et al., Stroke, Vol.35, 2004, pp.2500-2505.
[2] 徳田茂史ら, 日本機械学会論文集(B編), 74 巻740 号(2008-4).
[3] F.Y.Liang, et al., J Biomech 42,692-704(2009)
[4] V. Milisic, et al., Math Model and Numer Anal 38,613-632(2004).