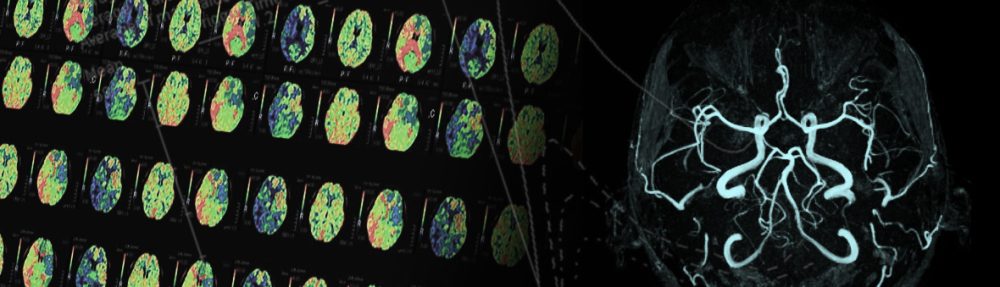
脳動脈瘤の発症や破裂には血流による壁面せん断応力などの力学的要因が関係すると言われている.生体内の壁面せん断応力などをシミュレーションによって正確に予測するためには生体内の血行動態を正確に再現する必要がある.一般的に血管壁は剛体ではなく,弾性を有する変形可能な組織として扱われ,血流の立場から見ると流路が変形することになる.生体内環境を忠実に模擬した血流シミュレーションを行うためにはこのような血管壁の変形も考慮する必要がある.そこで本研究では血流による流体力と血管壁の変形の相互作用を再現する流体構造連成解析を行う.
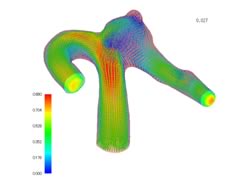
以下に示す図1は患者の医用画像から得られた中大脳動脈瘤における流体構造連成解析の流速ベクトルの結果の可視化である.この図より瘤内では流速の遅い血液が多いことがわかる.
Fig.1 中大脳動脈瘤内の流速ベクトル
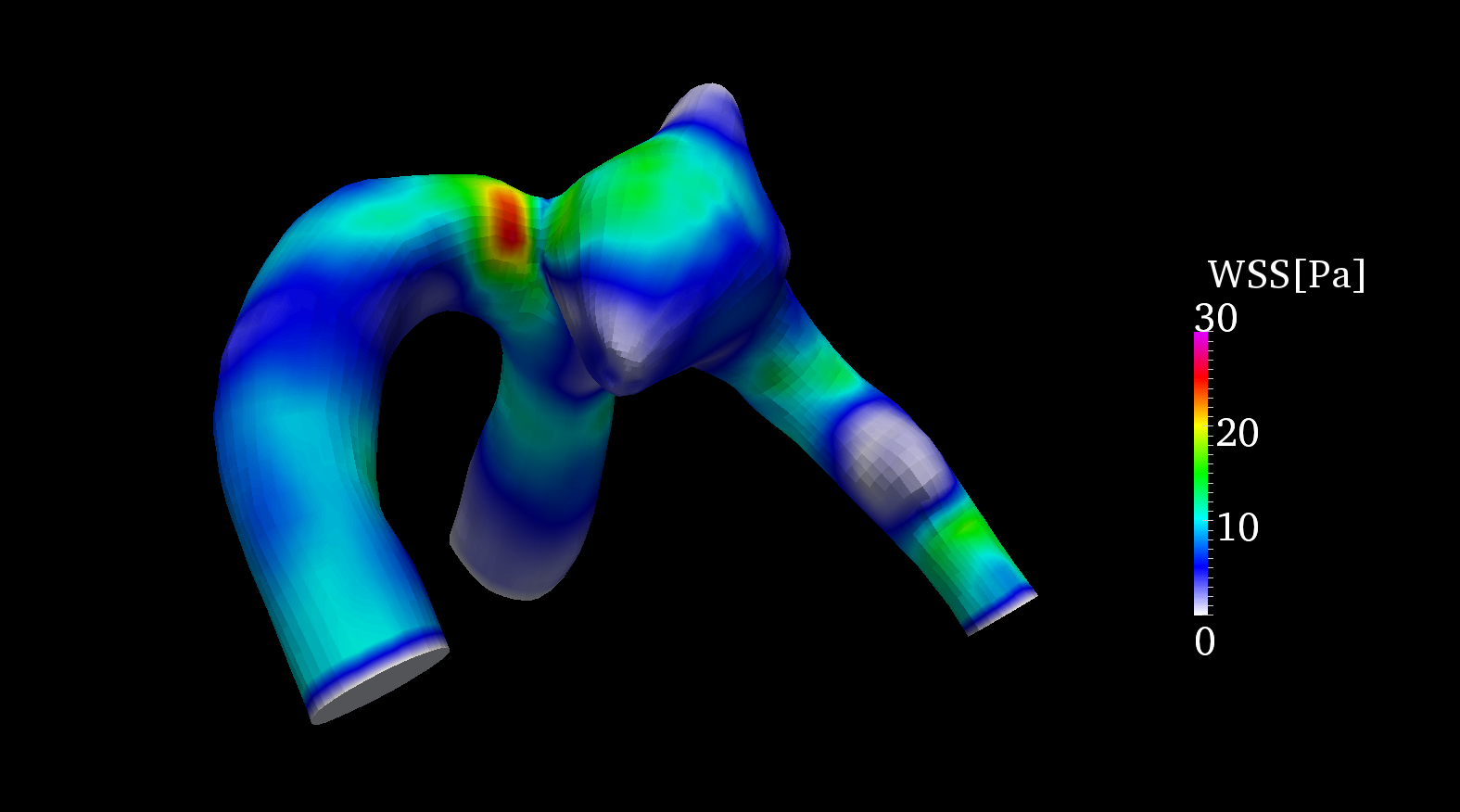
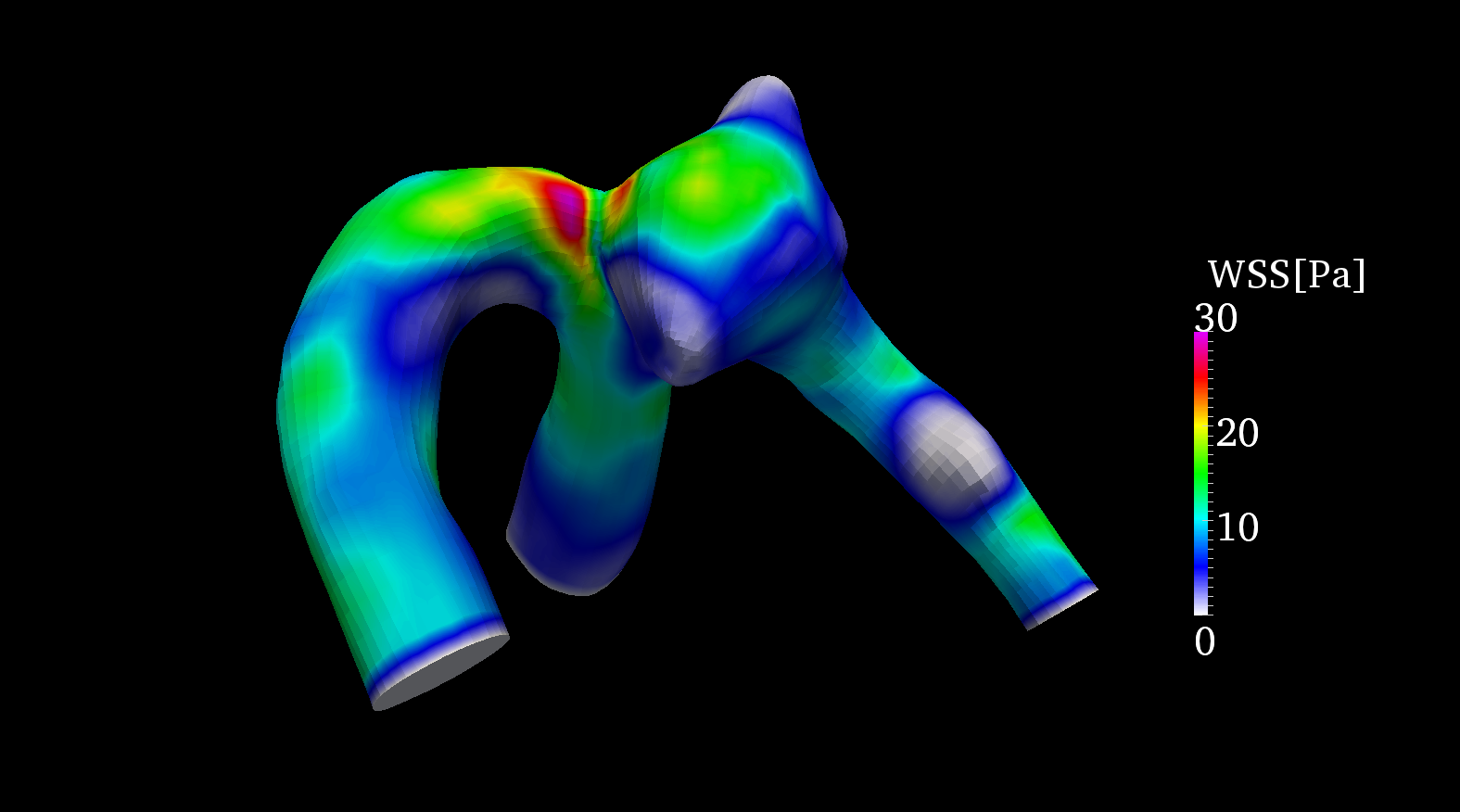
図 2,3には中大脳動脈瘤のシミュレーション結果から得られた拍動ピーク時の壁面せん断応力の分布を示している.図2は流体構造連成解析(FSI:Fluid Structure Interaction)の結果,図3には流体のみの解析結果を示す.図のように流体のみの解析と血管壁の変形を考慮した流体構造連成解析では壁面せん断応力の分布の様子が違うことがわかる.特に瘤のネック部において壁面せん断応力の分布の勾配が顕著に違う結果が得られた.
Fig. 2 流体構造連成解析 Fig. 3 流体解析
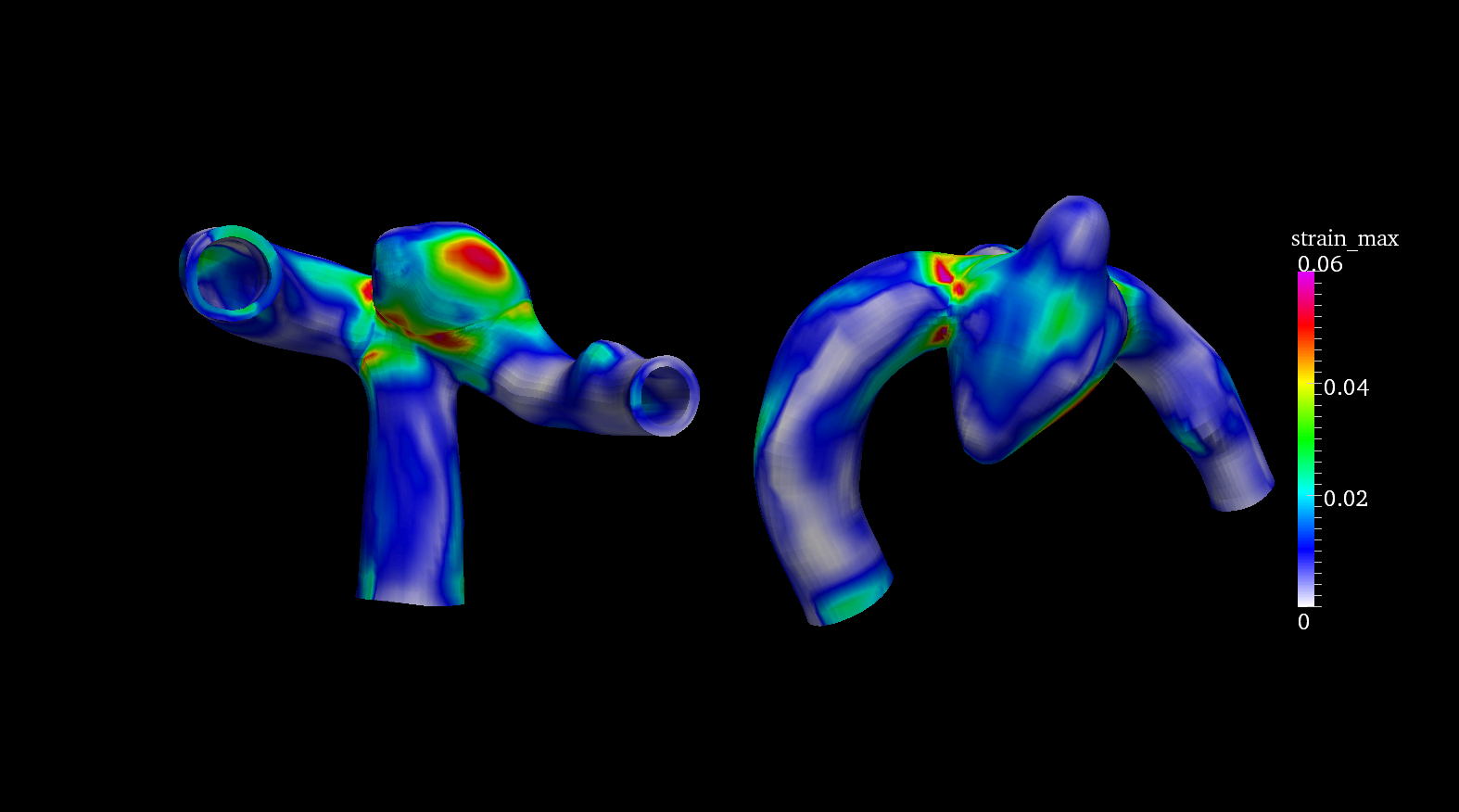
図4は拍動ピーク時の血管壁の最大主ひずみの分布をプロットしている.このように流体構造連成解析では流体のみでなくひずみや応力といった構造の指標も評価することができる.この図ではひずみは瘤の付け根のネック部に強く出ていることがわかる.
Fig.4 拍動ピーク時の最大主ひずみ分布
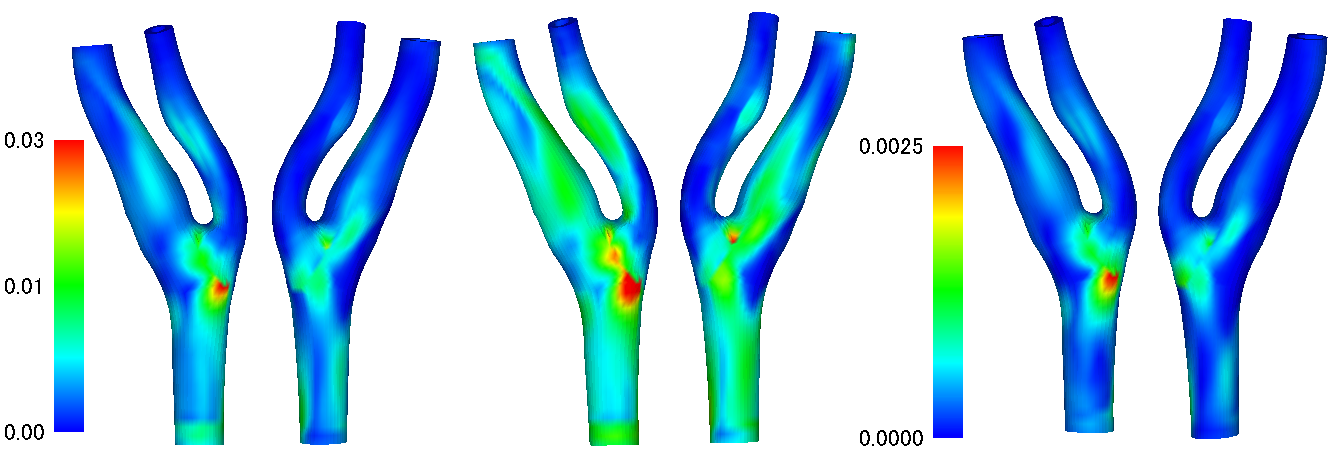
流体構造連成解析では構造部の材料特性も重要である.一般に血管壁の材料特性は非線形の超弾性体であると言われており,応力とひずみの関係が線形ではない.上図の中大脳動脈瘤の解析ではMooney-Rivlin体と呼ばれる非圧縮超弾性体モデルを採用した.以下に示す図5では頸動脈において超弾性体のモデルを変えて構造解析を行った結果である.用いる材料モデルによって得られる変位の大きさや,分布が大きく変わることがわかる.
Fig.5 頸動脈における変位分布(材料モデルによる違い)
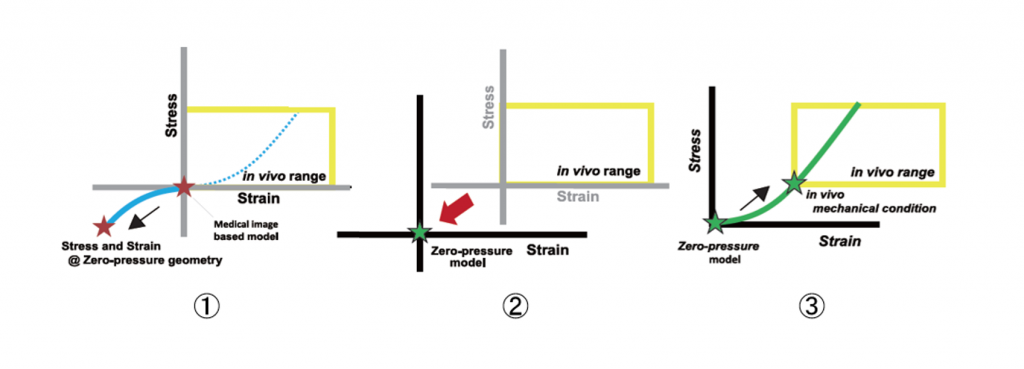
流体構造連成解析における血管壁の変形挙動は,医用画像取得時の血管形状における応力状態によって大きく変化しうるが,応力状態を計測することが不可能であるため初期条件の設定が難しい.負圧負荷によって血圧無負荷状態の血管形状を推定することで応力状態の初期条件を設定する手法を図6に示す.血管壁の材料特性を,応力―ひずみ関係が原点において対称となる非線形弾性材料として仮定し,医用画像取得時の血圧に相当する負圧を血管内壁に一様に加える(①).その後血管壁内に生じた応力,ひずみをリセットし(②),改めて血圧相当の圧力を血管壁一様に負荷することで(③),医用画像取得時の血管形状における応力状態を再現する.
Fig.6 負圧負荷による血圧無負荷状態の血管形状の推定法
参考文献
1. 片桐賢吾, 石上雄太, 大島まり, 山本創太, 流体-構造連成手法を用いた患者個体別頸動脈の解析, 第26回数値流体シンポジウム(東京2012)
2. Ryo Torii, et al., Int. J. Numer. Methods Fluids, Vol. 65, ( 1-3):pp.324-340, 2011.